数据结构之二维数组
本文最后更新于 2025-10-16,文章内容可能已经过时。
一、二维数组
int[][] array = {
{10, 12, 14, 16, 18},
{20, 22, 24, 26, 28},
{30, 32, 34, 36, 38},
};
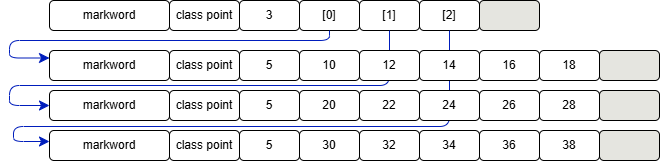
内存图如下
-
二维数组占 32 个字节,其中 array[0],array[1],array[2] 三个元素分别保存了指向三个一维数组的引用
-
三个一维数组各占 40 个字节
-
它们在内层布局上是连续的
在编程语言中,当我们定义一个二维数组 a[m][n] 时,这里的 m 和 n 分别代表了二维数组的两个维度大小。具体来说:
m表示的是二维数组的行数(即第一维的大小),也就是该数组包含多少个一维数组。n表示的是每一行中的元素数量,也即是列数(即第二维的大小),也就是说每个一维数组中有多少个元素。
因此,a[m][n] 定义了一个具有 m 行和 n 列的矩阵或表格结构。
int a[3][4];
创建了一个拥有 3 行 4 列的整型二维数组,意味着这个数组总共可以存储 12 个整数值,按照先行后列的方式排列。当涉及到访问这样的二维数组时,可以通过指定行列索引来获取特定位置上的值。例如,要访问上面定义的二维数组 a 中第 i 行第 j 列的元素(假设 i 和 j 的值都在有效范围内),你可以使用表达式 a[i][j]。需要注意的是,数组索引通常是从 0 开始计数的,所以第一个元素的位置是 a[0][0],而最后一个元素如果是 3x4 的数组,则位于 a[2][3]。
Java 环境下(不考虑类指针和引用压缩,此为默认情况),有下面的二维数组
byte[][] array = {
{10, 12, 14, 16, 18},
{20, 22, 24, 26, 28},
{30, 32, 34, 36, 38},
};
已知 array 对象起始地址是 0x1000,那么 24 这个元素的地址是什么?
- 起始地址 0x1000
- 外层数组大小:16字节对象头 + 3元素 * 每个引用4字节 + 4 对齐字节 = 32 = 0x20
- 第一个内层数组大小:16字节对象头 + 5元素 * 每个byte1字节 + 3 对齐字节 = 24 = 0x18
- 第二个内层数组,16字节对象头 = 0x10,待查找元素索引为 2
- 最后结果 = 0x1000 + 0x20 + 0x18 + 0x10 + 2*1 = 0x104a
二、局部性原理
局部性原理(Principle of Locality)是计算机科学中的一个核心概念,它描述了程序访问内存时表现出的一种倾向或模式。根据这一原理,程序倾向于在一段时间内集中访问某些特定区域的存储单元,而不是随机地访问整个地址空间。这种现象可以分为几种不同类型,但最常见的是时间局部性和空间局部性。
时间局部性(Temporal Locality)
时间局部性指的是如果某个信息项已经被访问过,那么在未来不久的时间内,该信息项很可能再次被访问。例如,在程序中存在大量的循环操作,这意味着一旦进入循环体内的指令被执行,它们将在短时间内频繁地被执行。此外,堆栈结构也容易产生时间局部性,因为最近调用的函数可能会很快返回,并且其使用的变量也会被重新访问。
空间局部性(Spatial Locality)
空间局部性意味着如果程序当前正在访问某个存储位置,则在接下来的一段时间里,它可能还会访问附近的存储位置。这通常发生在指令顺序执行的情况下,因为大多数情况下,下一条要执行的指令位于当前指令之后的一个固定偏移量处;同样地,当处理数组或其他连续存储的数据结构时,会依次访问相邻元素。
除了上述两种主要形式外,还有其他类型的局部性:
- 顺序局部性(Order Locality):指除转移类指令外,大部分指令是按顺序进行的,顺序执行和非顺序执行的比例大约为5:1。此外,对大型数组访问也是顺序的。
- 内存局部性(Memory Locality):这是空间局部性的具体表现形式之一,特别是在讨论如何管理内存时使用。它强调了访问内存时,大概率会访问连续的块而非单一的内存地址。
- 分支局部性(Branch Locality):与顺序局部性类似,尽管存在条件分支,但在实际运行中,某些分支路径往往比其他路径更常被执行,因此可以通过预测这些模式来优化性能。
- 等距局部性(Equidistant Locality):当访问模式呈现周期性特征时出现,比如访问多个相同格式的数据结构,其中每次只取一部分字段,导致它们之间存在固定的间隔距离。
局部性原理的应用
局部性原理广泛应用于计算机系统的设计与优化之中,包括但不限于以下几个方面:
- CPU缓存设计:为了提高数据访问速度,现代CPU配备了多级缓存。通过利用时间局部性和空间局部性,可以将最近或即将使用的数据保存在靠近处理器的核心存储器中,从而减少访问主存所需的时间。
- 磁盘缓存/操作系统页面调度算法:操作系统利用局部性原理来决定哪些页面应该保留在物理内存中,哪些可以暂时交换到磁盘上,以确保常用的数据总是能够快速获取。
- 分布式系统中的缓存策略:像Redis这样的内存数据库服务以及内容分发网络(CDN),都是基于局部性原理构建起来的,目的是为了减轻后端服务器的压力并加快响应时间。
- Java JIT编译器:即时编译器(JIT Compiler)通过分析程序运行期间的行为,识别出热点代码段,并对其进行优化,使得这部分代码可以在后续执行过程中更加高效。
总之,局部性原理不仅是理解计算机架构和操作系统工作方式的关键,而且对于编写高效程序、设计高性能系统有着重要的指导意义。通过合理地应用局部性原理,我们可以显著提升系统的整体性能,同时降低成本。
实践之空间局部性
- cpu 读取内存(速度慢)数据后,会将其放入高速缓存(速度快)当中,如果后来的计算再用到此数据,在缓存中能读到的话,就不必读内存了
- 缓存的最小存储单位是缓存行(cache line),一般是 64 bytes,一次读的数据少了不划算啊,因此最少读 64 bytes 填满一个缓存行,因此读入某个数据时也会读取其临近的数据,这就是所谓空间局部性
import org.junit.jupiter.api.DisplayName;
import org.junit.jupiter.api.Test;
import org.springframework.util.StopWatch;
public class JBXYLTest {
@Test
@DisplayName("局部性原理示例")
public void test1() {
int rows = 10000000;
int columns = 16;
int[][] a = new int[rows][columns];
StopWatch sw = new StopWatch();
sw.start("ij");
ij(a, rows, columns);
sw.stop();
sw.start("ji");
ji(a, rows, columns);
sw.stop();
System.err.println(sw.prettyPrint());
}
/**
* ij 方法
* @param a
* @param rows
* @param columns
*/
public static void ij(int[][] a, int rows, int columns) {
long sum = 0L;
for (int i = 0; i < rows; i++) {
for (int j = 0; j < columns; j++) {
sum += a[i][j];
}
}
System.out.println(sum);
}
/**
* ji 方法
* @param a
* @param rows
* @param columns
*/
public static void ji(int[][] a, int rows, int columns) {
long sum = 0L;
for (int j = 0; j < columns; j++) {
for (int i = 0; i < rows; i++) {
sum += a[i][j];
}
}
System.out.println(sum);
}
}
0
0
StopWatch '': 0.9353496 seconds
----------------------------------------
Seconds % Task name
----------------------------------------
0.1262374 13% ij
0.8091122 87% ji
可以看到 ij 的效率比 ji 快很多,为什么呢?
- 缓存是有限的,当新数据来了后,一些旧的缓存行数据就会被覆盖
- 如果不能充分利用缓存的数据,就会造成效率低下
在讨论 ij 和 ji 两种遍历二维数组的方式时,我们需要理解局部性原理(Locality of Reference),特别是空间局部性(Spatial Locality)。根据局部性原理,当CPU访问一个内存位置后,它很可能很快就会再次访问该位置附近的内存。这是因为程序倾向于重复访问相同的内存区域或顺序地访问相邻的内存地址。
对于二维数组,ij 方法(外层循环遍历行)和 ji 方法(外层循环遍历列)对缓存的影响是不同的。具体来说:
ij方法:这种遍历方式按照数组存储的自然顺序进行读取,即按照行优先的方式访问元素。由于大多数编程语言(如Java、C/C++)中的二维数组是以行为主序存储的,这意味着每一行的数据都是连续存储在内存中的。因此,当使用ij遍历时,CPU能够有效地利用缓存行(Cache Line),每次加载不仅会取得当前需要的数据,还会预先加载其后的几个数据项。这减少了缓存未命中(Cache Misses)的情况,提高了性能。ji方法:相比之下,ji方法则以外层循环遍历列为起点。在这种情况下,虽然最终也会访问到所有的元素,但每次访问的是不同行同一列的元素。由于这些元素并不一定是在内存中连续存放的(特别是在大型矩阵中),这就导致了频繁的缓存行切换,增加了缓存未命中的次数,进而降低了效率。例如,在执行第一次内循环时读入[0,0],同时也会读入其邻近的数据[0,1]...[0,15];然而,第二次内循环所需的[1,0]数据不在已加载的缓存行中,因此必须从主存重新加载新的缓存行。
为了更直观地展示 ij 方法和 ji 方法在遍历二维数组时的行为差异,我们可以使用表格来表示这两种方法访问内存的方式。下面的表格将帮助解释为什么 ij 方法通常比 ji 方法更加高效,特别是在考虑缓存机制的情况下。
表格说明
假设我们有一个简单的 4x4 的二维数组(矩阵),并且该数组是以行优先的方式存储在内存中的。我们将通过表格的形式展示两种遍历方式如何读取这些数据,并标记出每次读取的数据是否已经在缓存中。
二维数组示例
| Index | Row 0 | Row 1 | Row 2 | Row 3 |
|---|---|---|---|---|
| Col 0 | 0 | 4 | 8 | 12 |
| Col 1 | 1 | 5 | 9 | 13 |
| Col 2 | 2 | 6 | 10 | 14 |
| Col 3 | 3 | 7 | 11 | 15 |
ij 方法:按行优先顺序遍历
当采用 ij 方法时,程序首先会从第一行开始,依次访问每一列的数据。由于数据是以行优先的方式存储,所以这种遍历方式可以充分利用CPU缓存,减少缓存未命中次数。
| Step | Access Pattern | Cache Line Hits/Misses |
|---|---|---|
| 1 | [0,0], [0,1], [0,2], [0,3] | Hit, Hit, Hit, Hit (First access misses) |
| 2 | [1,0], [1,1], [1,2], [1,3] | Miss, Hit, Hit, Hit |
| 3 | [2,0], [2,1], [2,2], [2,3] | Miss, Hit, Hit, Hit |
| 4 | [3,0], [3,1], [3,2], [3,3] | Miss, Hit, Hit, Hit |
在这个过程中,除了首次加载某一行的第一个元素会导致缓存未命中外,后续对该行其他元素的访问都可以命中缓存,因为它们已经被加载到了同一个缓存行中。
ji 方法:按列优先顺序遍历
相反地,ji 方法是从第一列开始,逐行向下读取同一列的数据。这种方式导致了更多的缓存未命中,因为它打破了数据在内存中的连续性,使得每次访问新的列都需要从主存重新加载数据。
| Step | Access Pattern | Cache Line Hits/Misses |
|---|---|---|
| 1 | [0,0], [1,0], [2,0], [3,0] | Miss, Miss, Miss, Miss |
| 2 | [0,1], [1,1], [2,1], [3,1] | Miss, Miss, Miss, Miss |
| 3 | [0,2], [1,2], [2,2], [3,2] | Miss, Miss, Miss, Miss |
| 4 | [0,3], [1,3], [2,3], [3,3] | Miss, Miss, Miss, Miss |
可以看到,ji 方法几乎每一次对新列的访问都会导致缓存未命中,这是因为不同行但相同列的元素并不位于相邻的内存位置上,从而降低了缓存的有效利用率。
性能影响
根据上述分析,我们可以得出结论:ij 方法更适合于以行优先方式存储的二维数组,因为它能够更好地利用缓存机制,减少缓存未命中的概率。相比之下,ji 方法则可能引发更多的缓存未命中事件,尤其是在处理大型矩阵时,这将显著降低程序的运行效率。
综上所述,选择适当的遍历顺序对于优化程序性能至关重要,尤其是在处理大规模数据集时。遵循空间局部性原则可以帮助减少不必要的缓存未命中,从而提升应用程序的整体性能。此外,这一概念不仅适用于内存访问模式,还可以扩展到磁盘I/O操作等领域。
举一反三
-
I/O 读写时同样可以体现局部性原理
-
数组可以充分利用局部性原理,那么链表呢?
答:链表不行,因为链表的元素并非相邻存储
- 感谢你赐予我前进的力量